正如 CPU 是现代计算中执行一切指令的基石,神经网络 (Neural Network) 则是驱动当前人工智能浪潮的“AI 处理器”。从智能手机的个性化推荐,到驱动大型语言模型的复杂算法,神经网络已无处不在。然而,许多人仍将 AI 视为一个即插即用的“黑盒”。对于渴望掌握核心技术的人来说,不深入其内部探寻原理,终究无法做到真正的游刃有余。因此,本文将化繁为简,如同拆解硬件一般,从最基础的单元——“神经元” (Neuron) 出发,层层深入,清晰地揭示神经网络的构造、学习机制,以及其“智能”的由来。
一、机器学习是什么?
传统程序的都是固定功能,固定形式,它可以是最基础,实现两个输入数字之和的脚本,也可以是复杂的,根据登陆用户的信息,查询数据库中的数据,返回对应用户信息后端服务,但是归根结底,这类程序的功能和性能,都是在代码书写阶段就固定了的。
但是机器学习不同,机器学习也是一类程序,但是它可以根据投喂的数据,慢慢学习数据中的规律,从而慢慢提高性能,这里借用大佬 汤姆·米切尔 在其1997年出版的经典教科书《机器学习》中对机器学习的定义:一个计算机程序被称为可以学习,是指它能够针对某个任务(T)和相应的性能评测(P),从 经验(E) 中学习,使其在任务T上的性能表现(以P为标准)随着经验E的增加而提高。(简单描述就是:一个程序能“学习”,指的是你给它提供越多的“案例”或“数据”,它在处理某个特定“工作”时,就会表现得越好、犯的错越少。)
现在 Google 或者 OpenAI 对于机器学习的定义会更具体一些:机器学习是人工智能(AI)的一个分支,它利用算法和统计模型,使计算机系统能够从数据中学习模式并做出预测或决策,而无需进行显式编程。
二、AI 的历史
理论起源:
1943年: 科学家沃伦·麦卡洛克和沃尔特·皮茨提出了第一个神经元数学模型,被认为是神经网络思想的起点。他们证明了由简单神经元组成的网络可以计算任何算术或逻辑函数。
机器学习萌芽(1950 ~ 1980):
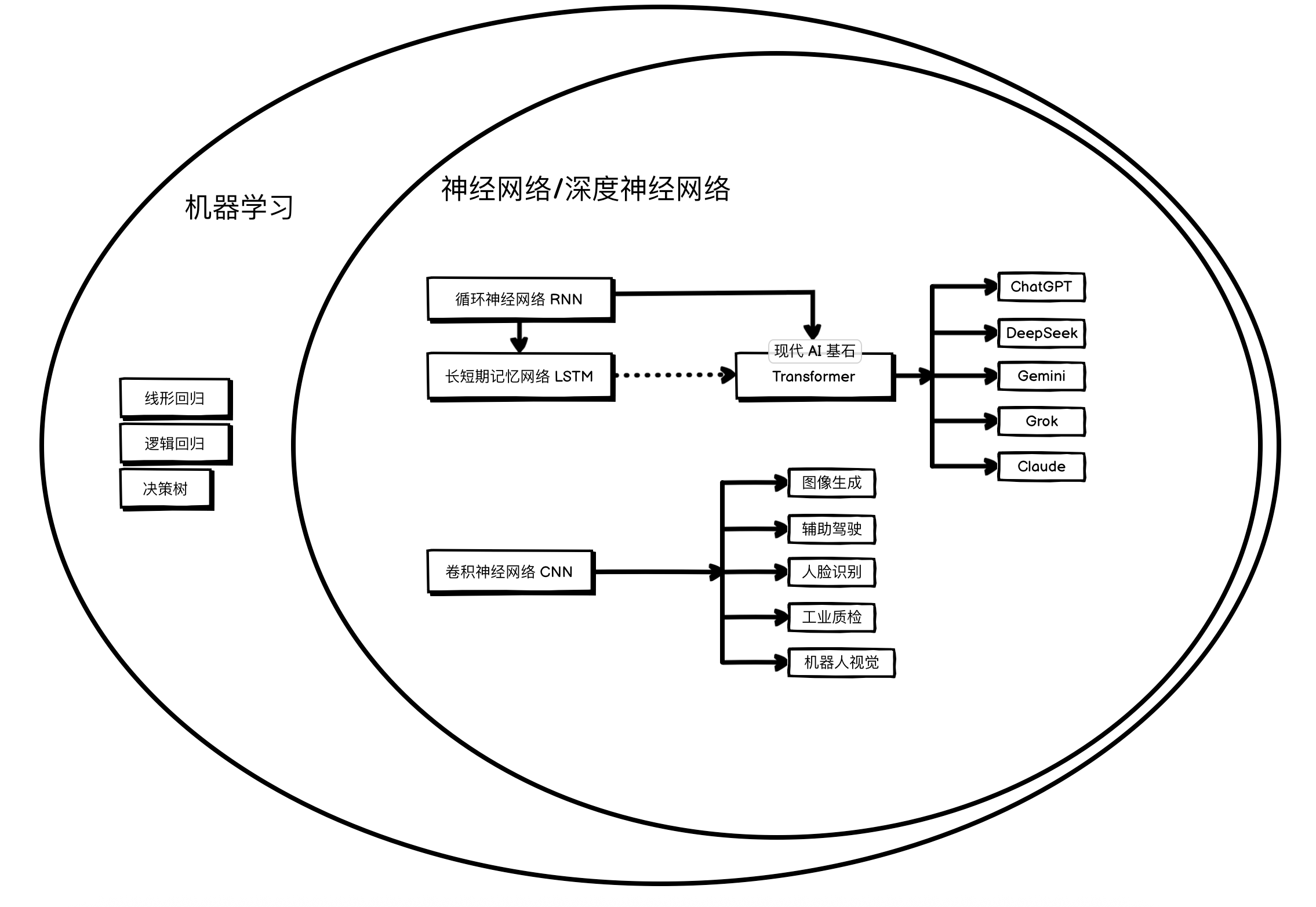
这个阶段有各种机器学习算法和模型相继问世,包括线性回归,逻辑回归,决策树等,同时,神经网络模型也在这个时期诞生。
- 1958年: 弗兰克·罗森布拉特发明了感知机 (Perceptron),这是第一个可以学习的、具体的神经网络模型。
关键算法的突破与发展 (1980 – 2000):
反向传播算法被发明,它高效地解决了训练多层神经网络的难题,让神经网络研究得以快速发展。CNN/RNN 也在这个时期被提出和实现。
这个时候:
- 1989-1998年: 杨立昆 (Yann LeCun) 开创性地提出了卷积神经网络 (Convolutional Neural Network, CNN),并在1998年开发出LeNet-5用于识别手写数字。CNN通过其“卷积”和“池化”操作,在处理图像这类网格状数据上展现出巨大优势。
- 1980s-1990s: 循环神经网络 (Recurrent Neural Network, RNN) 的思想被提出和发展,它通过内部的“循环”结构来处理序列数据(如文本、语音)。但它存在“长期依赖”问题(难以有效记忆)。
- 1997年: 为了解决RNN的长期依赖问题,赛普·霍克赖特 (Sepp Hochreiter) 和于尔根·施密德胡伯 (Jürgen Schmidhuber) 发明了长短期记忆网络 (Long Short-Term Memory, LSTM)。这是一种特殊的RNN,通过精巧的“门控”机制,可以有效地学习和记忆序列中的长期信息。
受限于算力和数据,神经网络在这个时期并没有表现出特别突出的价值。
深度学习革命 (2010 - 2017) :
2012年: AlexNet(一个深度卷积神经网络)在ImageNet图像识别大赛中以压倒性优势夺冠,其错误率远低于传统方法。这一年被广泛认为是深度学习革命的引爆点。
成功的关键因素:
- 大数据: ImageNet等大规模标注数据集的出现。
- 大算力: GPU并行计算能力的飞速发展。
- 好算法: CNN、LSTM等早已发明的算法终于有了用武之地。
AlexNet 的巨大成功,使神经网络重新获得了学术界和工业界的广泛关注。并且,随着大数据和GPU算力的成熟,此前制约其发展的两大瓶颈得以突破,神经网络也由此大举从学术界迈向工业界。
Transformer 时代 (2017 - 至今):
Transformer以其更高效、更强大的架构,取代了 LSTM ,开启了现代大语言模型和生成式AI的新纪元。
2017年: 谷歌发布了里程碑式的论文《Attention Is All You Need》,提出了Transformer模型
- 核心创新: 它完全抛弃了RNN/LSTM的循环结构,仅使用一种名为“自注意力机制 (Self-Attention)”的结构来处理序列数据。这使得模型可以并行计算(比RNN快得多),并且能更有效地捕捉序列中的长距离依赖关系。
- 巨大影响: Transformer架构迅速成为自然语言处理(NLP)领域的绝对主宰,并为后续一系列主流的大语言模型(LLM),如 BERT/Gemini 和 GPT 系列奠定了基础。它的影响力还扩展到了计算机视觉等其他领域。
到现在为止,所有主流大模型,基本都是以堆叠 Transformer 中 Decoder 模块实现。
三、线性回归
线性回归,顾名思义,当结果有线性关系的时候,可以用线性回归来总结。最简单的,一辆汽车的载货量和油耗就可以用线性关系来表示,并且是最简单的简单线性回归。
还有房屋价格预测,这种会跟多种属性挂钩,例如房屋面积、房间数量、房屋年龄、距离地铁站距离等,以多种数据,得到单一结果这种预测行为,也叫多元线性回归。
这里用简单线性回归来展示线性回归是如何“学习”数据集中的特征的。
首先生成数据:
import numpy as np
# 1. 生成一段基础数据
label = np.arange(0, 100, 0.1)
# 生成噪点,目标为 -1 ~ 1 。
noise_on_label = (np.random.random([1000]) * 2) - 1
label = label + noise_on_label
#print(label)
# 2. 从 0 到 999 的索引中,随机选择 50 个不重复的索引
# label.shape[0] 会得到数组的长度,即 1000
# replace=False 确保选出的索引是唯一的
indices_to_keep = np.random.choice(label.shape[0], 50, replace=False)
# 3. 使用这些随机索引来创建新的、清理后(只保留50个)的数组
label = label[indices_to_keep]
# 创造一个有噪点的乘数,值为 10 前后浮动 1 。
multiplier_data = np.array([10] * 50)
noise_on_multiplier = (np.random.random([50]) * 2) - 1
multiplier = multiplier_data + noise_on_multiplier
# 生成 target 。
target = label * multiplier
这个数据集,label 是 50 个值,随机分布在 0 到 100 。
然后 target 跟 label 挂钩,但是不是纯线性,加了噪点。
这里直接查看数据图:
import matplotlib.pyplot as plt
# 绘制散点图
plt.scatter(label, target, alpha=0.7)
# 坐标轴名称
plt.xlabel("label")
plt.ylabel("target")
# 保存图片
plt.savefig('label_target_scatter_plot.png')
得到数据图:
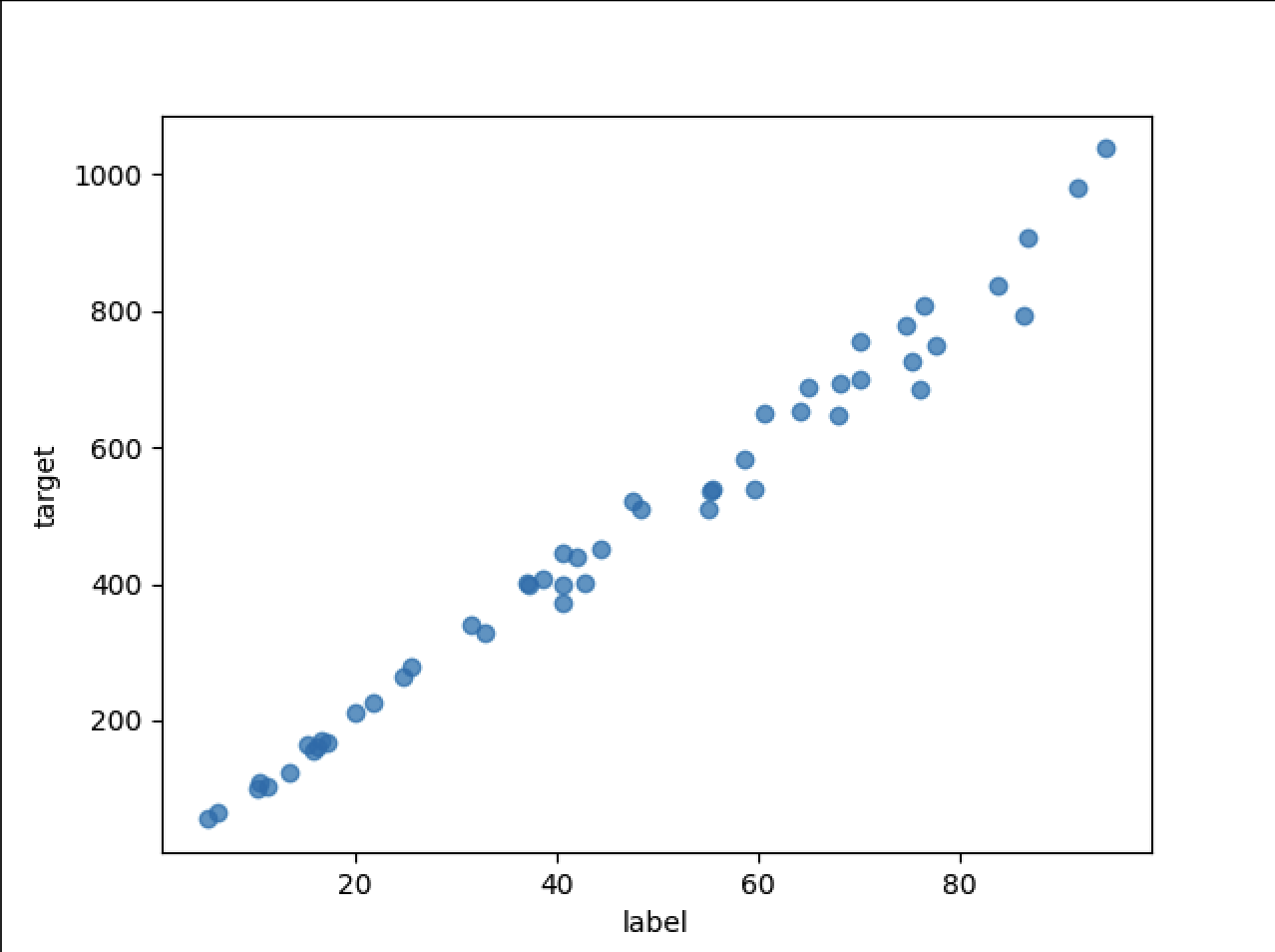
现在我们有了数据,但是还有一个问题,机器如何“学习”这个数据的规律呢?
在当前一元场景中,我们假设,label 为 x,target 为 y。
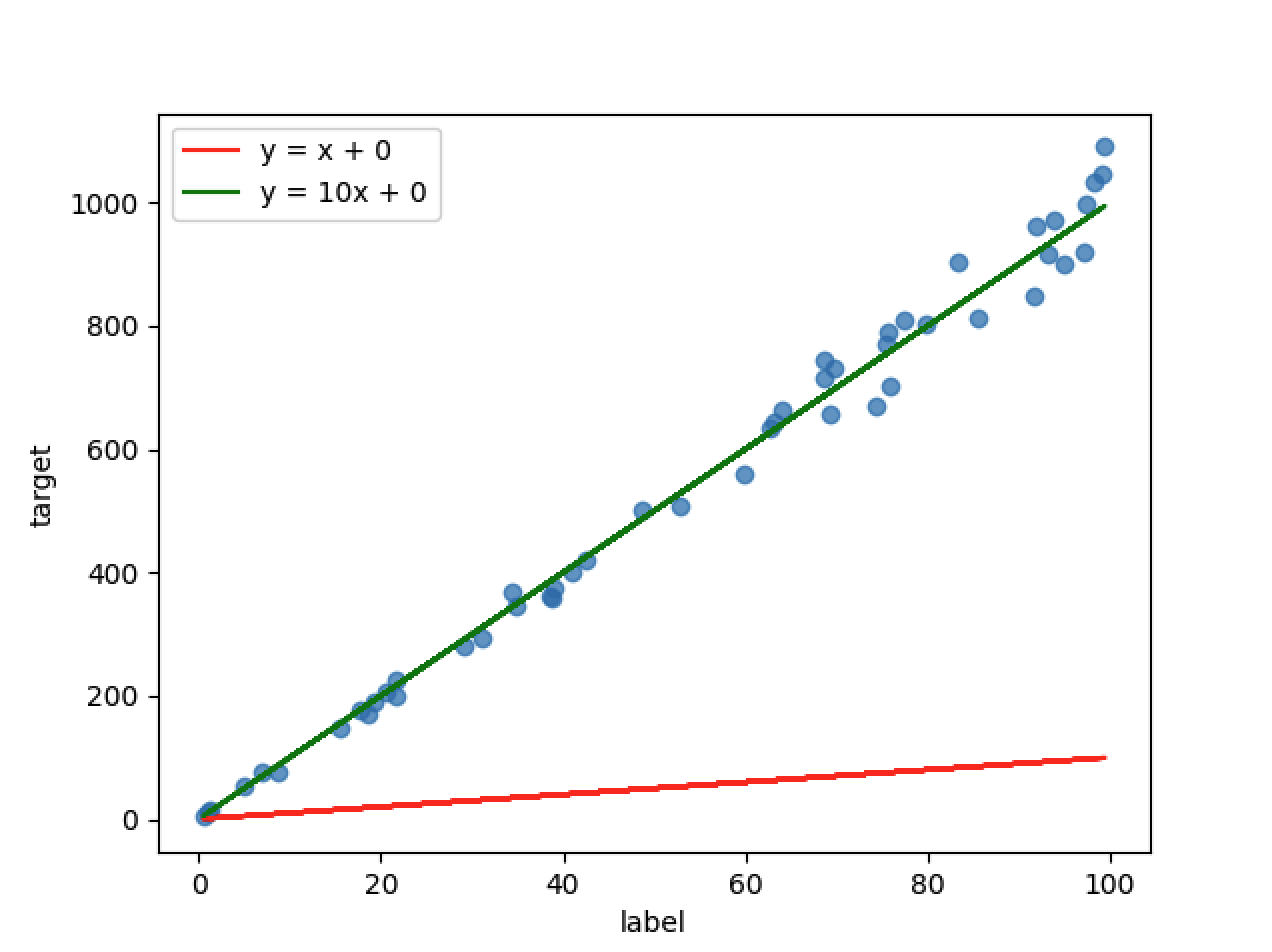
按我们数据集来源,我们可以得出 y=10x (虽然有噪点,但是数据拟合本身就是抽取特征,不可能 100% 准确。)。
这样会有两个问题:
- y=wx 这种函数有什么问题?
- 把数据喂给程序,程序如何得出 y=10x 这样的结果出来?
问题1: y=wx 有什么问题?
- y=wx 这种函数,将会有一个隐含条件,x=0 时,y也需要等于 0 。
所以当我们的数据集不经过 (0, 0) 时,整个逻辑就无法实现了。
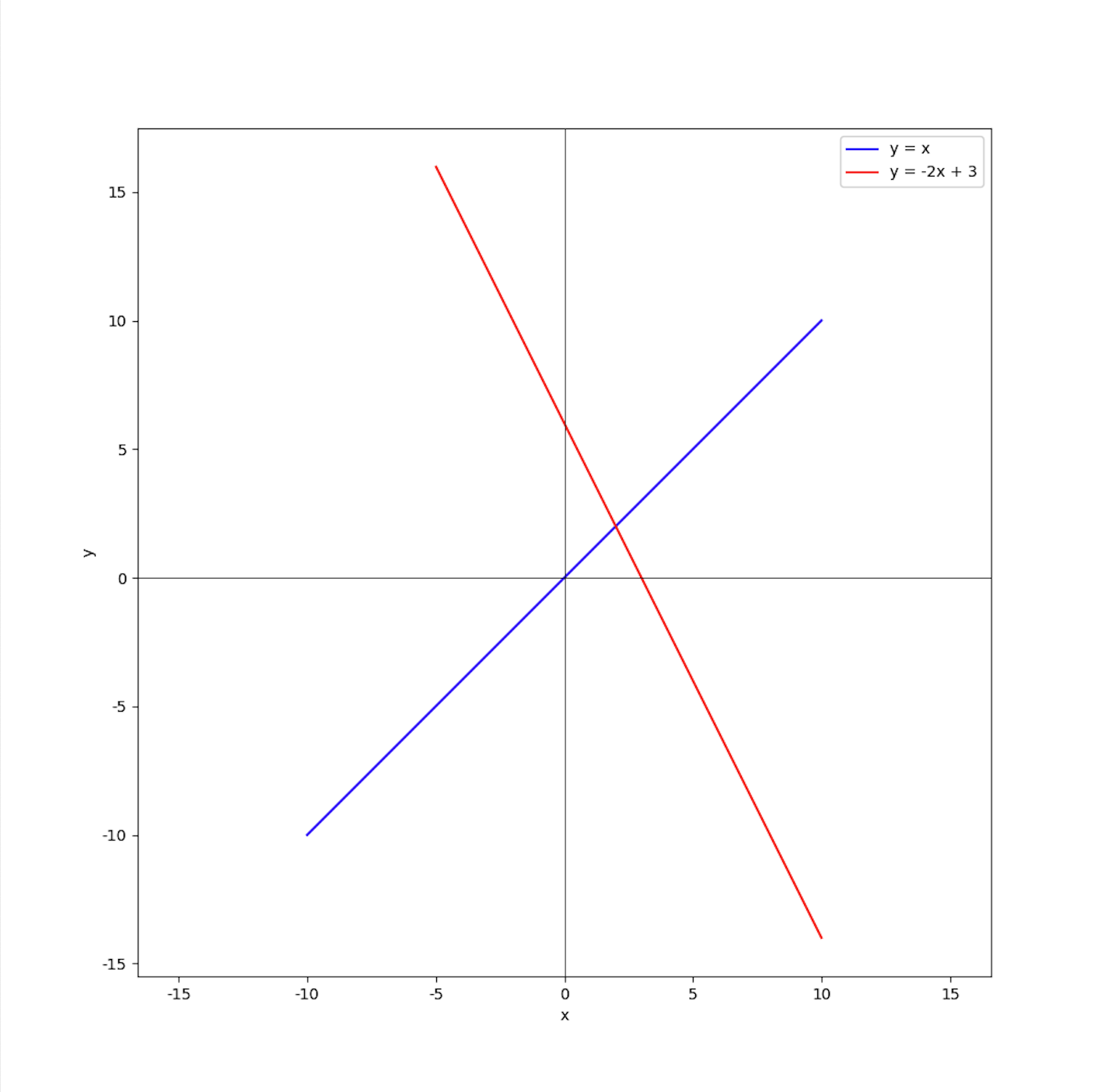
当需要描绘 y=-2x + 3 这样的特征的时候,就需要增加一个参数。
即: y=wx + b ,这里,w为权重,b 为偏置,不管是在当前线性回归场景,还是在后续神经网络中,都有此概念。
问题2: 把数据喂给程序,程序如何得出 y=10x + 0 这样的结果出来?
-
初始模型与预测
我们从一个最简单的线性模型
y = w * x + b开始。将权重w和偏置b初始化为 0,此时模型为y = 0 * x + 0。现在,我们使用一组数据来训练模型:当输入
x = 1时,真实的输出y_true = 10。我们将x=1代入当前模型,得到预测值y_pred = 0 * 1 + 0 = 0。但是真实值 y_true 为 10 。中间有差距,要缩小差距。
-
定义并计算损失:
损失函数有很多种,核心功能是计算预测和真实结果直接的差异,并更好的调整权重和偏置。
主流的有两种:
- 均方误差 MSE:
Loss = (y_true - y_pred) ^ 2 - 绝对值误差 MAE:
Loss = abs(y_true - y_pred)
这里以均方误差 MSE 举例子,主要是因为均方误差和梯度下降组合比较合适(均方误差会在误差越大的时候,损失越大,从而更快的调整权重和偏置,当误差小的时候,损失也越小,从而越精确的调整权重和偏置。),并且应用的也更多。
损失为:
Loss = (10 - 0) ^ 2 = 100 - 均方误差 MSE:
-
计算梯度(反向传播)
计算dL/dw:权重 w 对 L 的斜率(导数),即权重对损失的影响。
权重对于损失的影响为
w → y_pred → Loss。即:
dL/dw = dL/dy_pred * dy_pred/dw分两部分计算:
-
dL/dy_pred(预测值对损失的影响)由
Loss = (y_true - y_pred) ^ 2可以得出:dL/dy_pred = 2 * (y_pred - y_true) = 2 * -10 = -20 -
dy_pred/dw(权重对预测值的影响)y_pred = w * x + b,由于 x 和 b 都是常数。得出:
dy_pred/dw = x = 1
得到
dL/dw = dL/dy_pred * dy_pred/dw = -20 * 1 = -20计算
dL/dw: 偏置 b 对 L 的斜率(导数)即:
dL/db = dL/dy_pred * dy_pred/db-
dL/dy_pred = -20 -
dy_pred/db:y_perd = w * x + b,由于 x 和 w 都是常数。即
y_perd = b,即dy_pred/db = 1
得到
dL/dw = -20 -
-
更新参数(梯度下降)
现在我们有了梯度,就可以更新
w和b了。我们引入一个超参数——学习率(Learning Rate,lr),它决定了我们每一步调整的幅度。这里我们设定lr = 0.1以方便演示。根据之前计算的斜率:
w = w - dL/dw * lr = 0 - (-20) * 0.1 = 2b = b - dL/db * lr = 0 - (-20) * 0.1 = 2
这样,经过一轮训练,我们的模型从
y = 0x + 0更新为y = 2x + 2。 -
验证训练效果
再次代入 x = 1 ,得到
y_pred = 2 * 1 + 2 = 4计算损失:
Loss = (10 - 4) ^ 2 = 36可以看到,损失从最初的 100 降低到了 36,模型确实在向正确的方向优化,只要重复这个过程,模型就会越来越接近真实的数据分布。
-
讨论:不同的梯度下降方法
但是一次性喂一个数据,这种方法叫做随机梯度下降 (SGD),噪点会对其产生较大影响,比如最后一个数据给的是(x = 10, y = 90),且学习率不低,那这样整个模型都会偏差很多。
比较通用的方案是小批量梯度下降 (Mini-Batch GD),把数据分成多批,分批训练。
还有一种方案为批量梯度下降 (BGD),即一次性训练所有数据,这个较少使用。
以上演示的是仅含单个特征的简单线性回归。在实际应用中,模型通常需要处理多个特征(如房价预测中考虑面积、楼层、地段等),这时便会使用多元线性回归。其公式扩展为:y = w1 * x1 + w2 * x2 + … + wn * xn + b
当然,机器学习的工具箱远不止于此。除了线性模型,还有支持向量机 (SVM)、决策树、随机森林等众多强大的算法,它们适用于不同类型的问题和数据结构,这里便不逐一展开了。
为什么是梯度下降
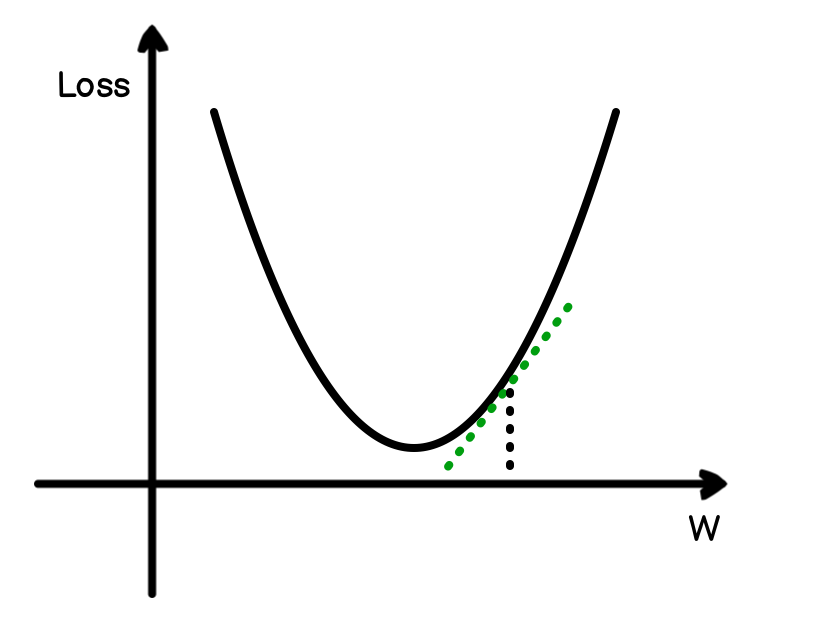
从 wx + b 的到预测值,预测值和真实值差的平方的到 Loss 来看,W 和 Loss 的函数会和上图类似,有一个 Loss 最低点,除此之外,往左或者往右,都会增加损失,如图标记点所示,计算出当前点的斜率,就可以知道,该以什么力度调整。
如图所示,绿色线就是在某个时刻的斜率,
四、神经网络
神经网络,又可称为前馈神经网络,或者全连接网络,可缩写为 MLP。
和其他机器学习算法或者模型相比,其他机器学习算法和模型,基本是一个固定框架的函数,它可以因为训练数据量不同,和输入输出节点的数量不同,从而呈现出不同的函数,但是究其根本,其还是在之前的基础的函数上进行扩展。而神经网络,只要神经元(节点)足够多,它就可以逼近任何连续函数。
神经网络的整个流程和线性回归区别不大,基本可以说是在线性回归的基础上再进行扩展。
而且线性回归可以算是神经网络的基础,神经网络最基本的神经元节点,就是 wx + b 。但是只有权重和偏置的神经网络,就算是层次再多,最后也会坍缩成线性,也就是 wx + b 。这里就不得不引入激活函数。
4.1 激活函数
激活函数会给神经网络引入非线性的能力。如果没有激活函数,无论神经网络有多少层,其输出都只是输入数据的线性组合,这样就无法学习和表示复杂的数据模式。激活函数的作用就是赋予模型拥有“掰弯”直线的能力,从而可以拟合任意复杂的形状。理论上已经证明,一个包含非线性激活函数的两层神经网络,就已经可以逼近任何连续函数。因此,选择合适的激活函数至关重要。
下面是几种在神经网络中常见的激活函数:
- Sigmoid函数:这是早期神经网络中最常用的激活函数之一。它能将任意输入值压缩到 (0, 1) 的区间内,非常适合用来表示概率,因此经常被用在二元分类问题的输出层。但它的主要缺点是在输入值过大或过小时,函数的梯度会趋近于零,导致“梯度消失”问题,从而使网络训练变得非常缓慢。
- Tanh (双曲正切) 函数:Tanh函数可以看作是Sigmoid函数的一个变种,它将输入值压缩到 (-1, 1) 的区间内。与Sigmoid相比,它的输出以0为中心(zero-centered),这使得它在大多数情况下比Sigmoid函数表现得更好。不过,它仍然存在梯度消失的问题。
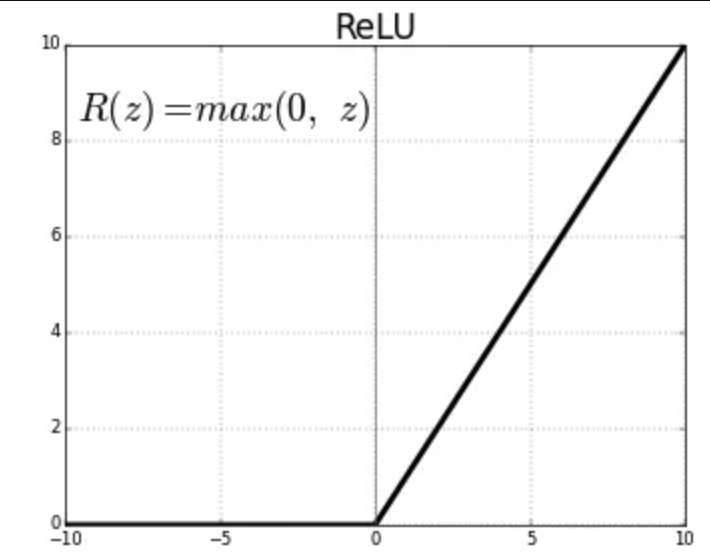
- ReLU (Rectified Linear Unit,修正线性单元):ReLU是目前深度学习领域最受欢迎的激活函数。它的规则非常简单:如果输入大于0,则输出就是输入本身;如果输入小于或等于0,则输出为0。这种简单的计算方式使得它的计算效率非常高,并且在很大程度上缓解了梯度消失问题,加快了网络的收敛速度。它的一个潜在缺点是,如果一个神经元的输入总是负数,那么它可能永远不会被激活,导致“神经元死亡”现象。
除了以上几种,还有 Leaky ReLU、ELU、Swish 等许多其他优秀的激活函数,它们分别对ReLU等函数的缺点进行了改进。
4.2 结构
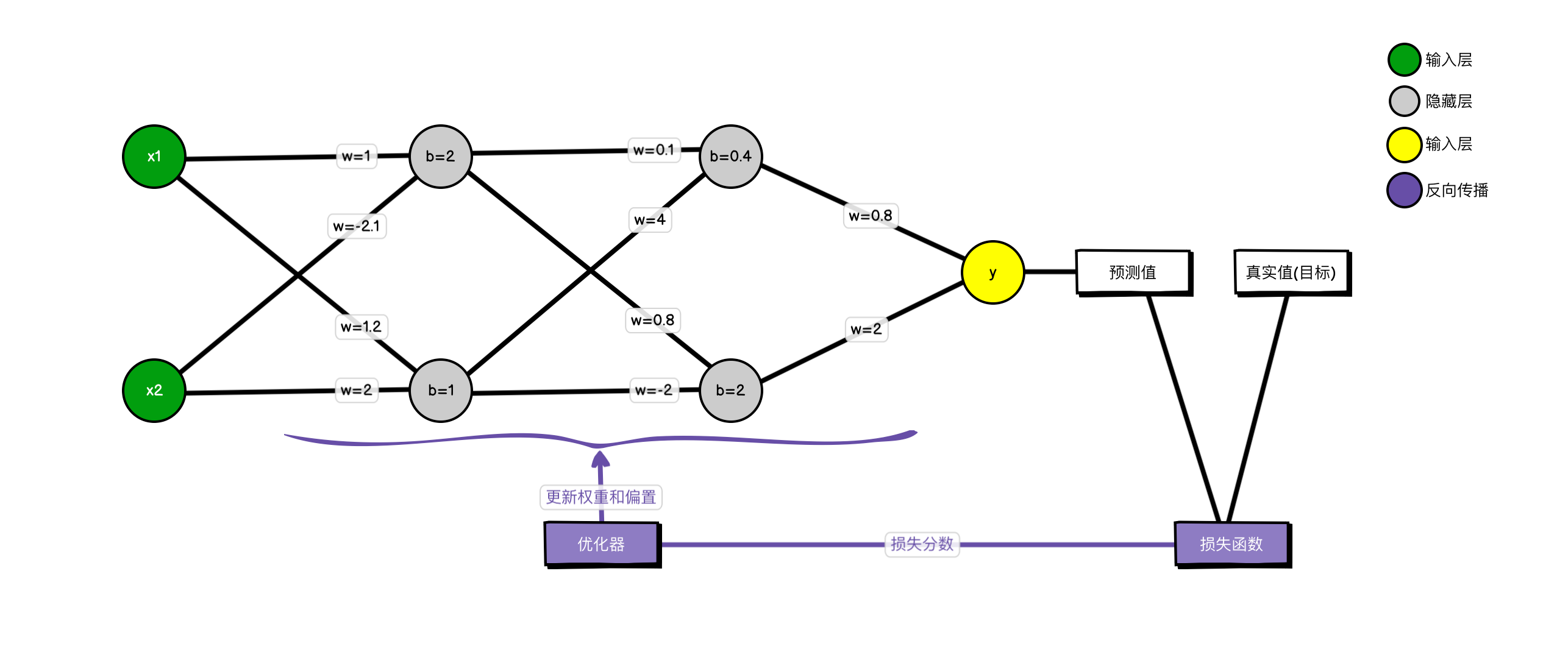
网络结构:
- 层级:网络由一个2节点的输入层(绿色)、两个各有2节点的隐藏层(灰色)和一个单节点的输出层(黄色)构成。
- 参数:连接各节点的线代表权重 (w),而隐藏层节点中的数值代表偏置 (b)。这些参数是网络学习的核心。
- 激活函数:虽然图中没有画出,但激活函数是隐藏层和输出层中必不可少的部分,用于进行非线性变换。
训练流程: 整个过程分为两个核心阶段:
- 前向传播 (从左至右):
训练数据(如
x1,x2)从输入层进入,依次流经两个隐藏层。在每个节点,输入信号会与对应的权重相乘,再加上偏置,然后(经由激活函数)计算出结果,并传递给下一层。最终,信号到达输出层,生成预测值 (y)。 - 反向传播与优化 (图中紫色部分):
- 首先,损失函数模块会对比模型的预测值和数据的真实值,计算出一个量化误差的损失分数。
- 然后,该损失分数被传递给优化器。
- 优化器采用梯度下降等算法,沿着能让损失降低最快的方向,反向计算并更新网络中每一个权重和偏置。
通过成千上万次重复“前向传播 → 计算损失 → 反向传播更新参数”的循环,网络中的权重和偏置被不断微调,最终学习到数据中蕴含的特征。这个包含了最优参数的完整网络,就构成了一个训练好的模型。
五、代码演示
5.1 创建数据集并图形化展示
# 导入用于数值计算的 numpy
import numpy as np
# 导入用于绘图的 matplotlib
import matplotlib.pyplot as plt
# 从 sklearn.datasets 中导入用于生成环形数据的函数
from sklearn.datasets import make_circles
print("工具已成功导入!")
# --- 生成数据集 ---
# X 是特征 (坐标), y 是标签 (属于哪个圆环, 0 或 1)
X, y = make_circles(n_samples=500, noise=0.1, factor=0.4, random_state=1)
# 我们将所有坐标值乘以 100
print("对数据进行人为的拉伸")
X = X * 100
Y = y * 100
# --- 查看一下数据长什么样 ---
print("数据集的形状:")
print(f"特征 X 的形状: {X.shape}") # 应该会输出 (500, 2)
print(f"标签 y 的形状: {y.shape}") # 应该会输出 (500,)
print("\n前5个数据点的坐标 (X):")
print(X[:5])
print("\n前5个数据点的标签 (y):")
print(y[:5])
############### 查看数据集 ##############
# 创建一个新的图形,设置它的大小
plt.figure(figsize=(8, 8))
# 绘制散点图
# X[:, 0] 是所有点的x坐标
# X[:, 1] 是所有点的y坐标
# c=y 告诉绘图工具根据标签y的值来着色
# cmap 是一个颜色映射,我们选择 'viridis' 或者 'RdYlBu' 都可以
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.viridis)
# 添加标题和坐标轴标签,让图表更清晰
plt.title("Dataset")
plt.xlabel("label (X-coordinate)")
plt.ylabel("target (Y-coordinate)")
# 显示网格线
plt.grid(True, linestyle='--', alpha=0.6)
# 显示图表
plt.show()
上面的代码可以生成一份相对而言较为复杂,不好用传统函数来拟合的数据集。
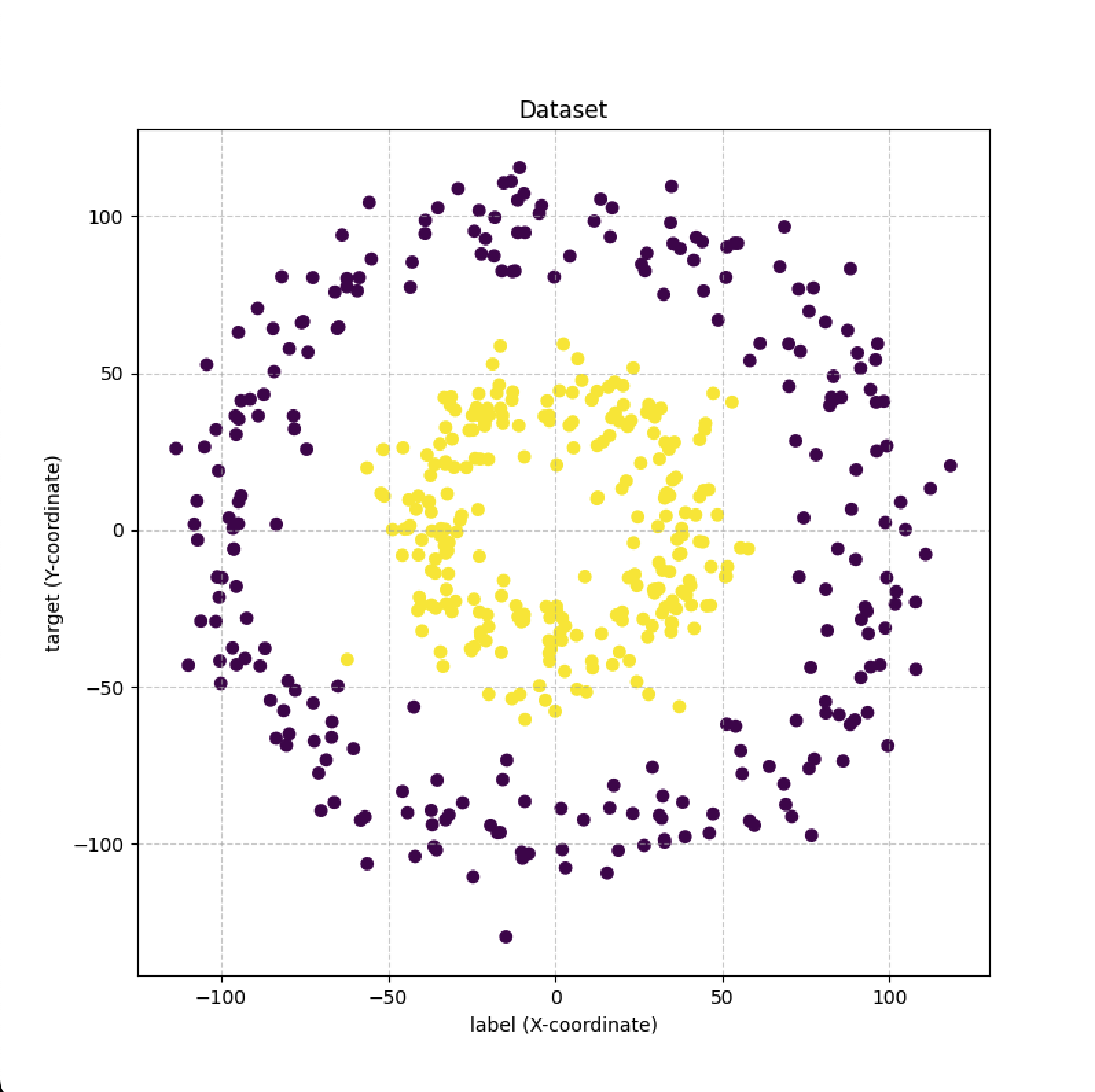
5.3 定义神经网络模型
###### 定义神经网络
# 从 sklearn.neural_network 导入 MLPClassifier
from sklearn.neural_network import MLPClassifier
# --- 定义模型 ---
print("\n正在定义神经网络模型...")
model = MLPClassifier(
hidden_layer_sizes=(10, 10, 10, 10),
activation='relu',
solver='adam',
max_iter=1000,
random_state=1
)
# hidden_layer_sizes=(10, 10, 10, 10): 4 个隐藏层,每个隐藏层 10 个节点。
# activation='relu' 激活函数为 rulu 。
# 使用 adam 优化器,它在绝大多数情况下都表现出色。
# 设置一个随机种子以保证模型初始化的权重是固定的,这样每次训练的结果都一样。
print("模型定义完成!结构如下:")
print(model)
上面定义了一个非常简单的神经网络,其隐藏层为 4 层,每层节点为 10 个。
5.3 训练
# 从 sklearn.preprocessing 导入 StandardScaler
from sklearn.preprocessing import StandardScaler
##### 划分数据集
from sklearn.model_selection import train_test_split
# --- 划分数据集 ---
print("\n正在划分数据集...")
# --- 划分数据 ---
# test_size=0.2 表示我们将20%的数据作为测试集
# random_state=42 保证每次划分的结果都一样
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
print("数据划分完成!")
print(f"训练集特征形状: {X_train.shape}")
print(f"测试集特征形状: {X_test.shape}")
# --- 正确地进行数据缩放 ---
# 1. 创建缩放器
scaler = StandardScaler()
# 2. 在训练集上进行拟合和转换
X_train_scaled = scaler.fit_transform(X_train)
# 3. 在测试集上只进行转换 (使用从训练集学到的规则)
X_test_scaled = scaler.transform(X_test)
print("\n数据缩放完成!")
# --- 训练模型 ---
# 注意:我们只在训练数据上进行 .fit()
print("\n在训练集上训练模型...")
model.fit(X_train_scaled, y_train)
print("模型训练完成!")
# --- 在测试集上评估模型 ---
accuracy = model.score(X_test_scaled, y_test)
print(f"\n模型在看不见的测试集上的准确率: {accuracy * 100:.2f}%")
通过把数据集拆分为测试集和训练集,在训练的时候使用训练集,在测试的时候使用测试集,这样就能清晰的验证模型的拟合情况,就能避免训练和测试都用同一个数据集,结果训练的模型过拟合。
5.4 可视化训练效果
##### 分开绘图
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
# --- 第7步 (最终版): 分开绘制训练集与测试集结果 ---
print("\n正在生成最终的可视化图表...")
# 1. 定义与您图片相似的颜色
# 我们选择深红色 (#8B0000) 和深蓝色 (#00008B)
custom_colors = ['#8B0000', '#00008B']
custom_cmap = ListedColormap(custom_colors)
# 2. 创建一个图,包含1行2列两个子图(axes)
# figsize=(16, 7) 让图更宽,以容纳两个子图
fig, axes = plt.subplots(1, 2, figsize=(16, 7))
# --- 准备决策边界的网格数据 (这部分和之前一样,只需计算一次) ---
h = .05
x_min, x_max = X_train_scaled[:, 0].min() - 1, X_train_scaled[:, 0].max() + 1
y_min, y_max = X_train_scaled[:, 1].min() - 1, X_train_scaled[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# 使用训练好的模型预测整个网格
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# --- 在第一个子图 (axes[0]) 上绘制训练集结果 ---
ax1 = axes[0]
# 绘制决策边界线
ax1.contour(xx, yy, Z, colors='black', linewidths=2)
# 绘制训练集的散点图
ax1.scatter(X_train_scaled[:, 0], X_train_scaled[:, 1], c=y_train, cmap=custom_cmap,
edgecolors='k')
ax1.set_title("Train Data", fontsize=15)
ax1.set_xlabel("x (Scaled)")
ax1.set_ylabel("y (Scaled)")
ax1.grid(True, linestyle='--', alpha=0.3)
# --- 在第二个子图 (axes[1]) 上绘制测试集结果 ---
ax2 = axes[1]
# 绘制完全相同的决策边界线
ax2.contour(xx, yy, Z, colors='black', linewidths=2)
# 绘制测试集的散点图
ax2.scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], c=y_test, cmap=custom_cmap,
edgecolors='k')
ax2.set_title("Test Data", fontsize=15)
ax2.set_xlabel("x (Scaled)")
ax2.grid(True, linestyle='--', alpha=0.3)
# 调整布局防止标题重叠
plt.tight_layout()
# 显示最终的图表
plt.show()
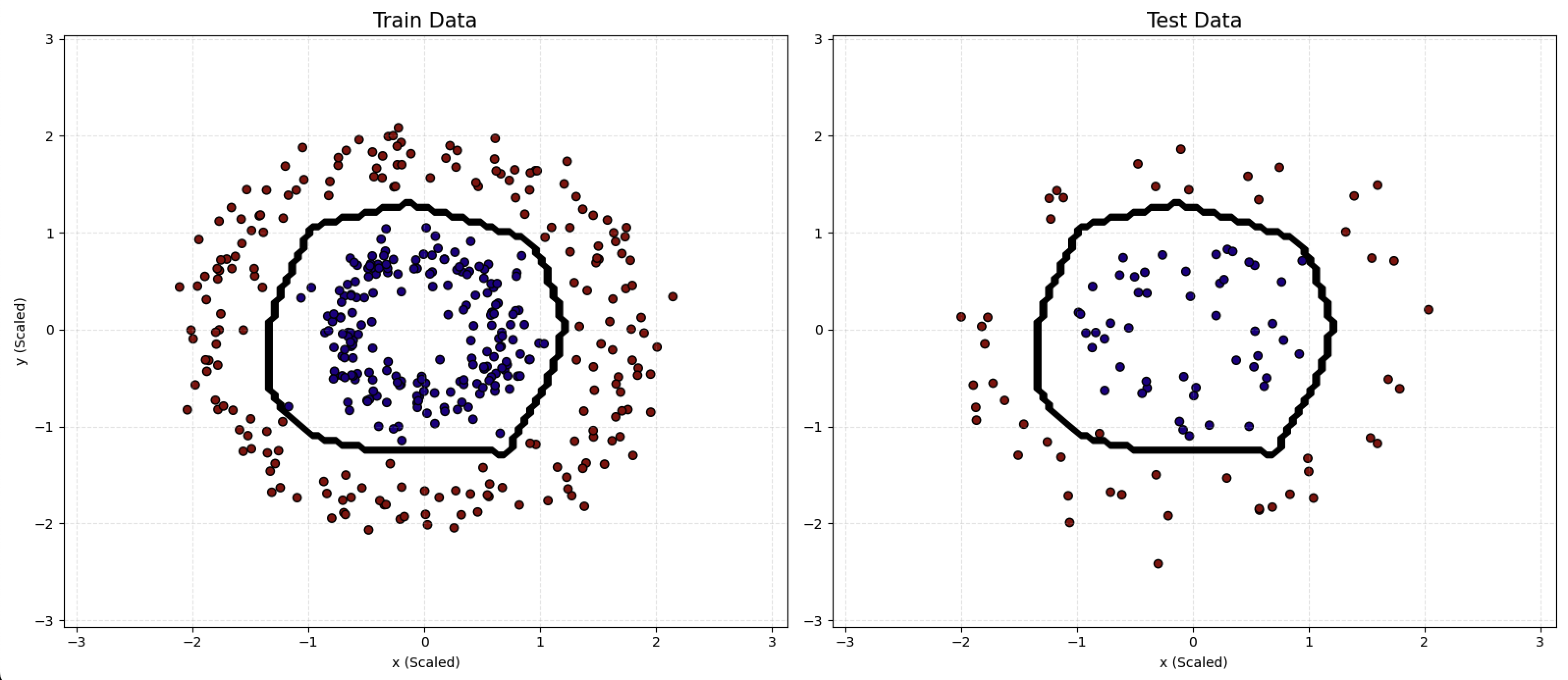
从图中可以看出,模型对训练集数据实现了良好拟合,并且在测试集上也达到了同样的效果。
总结
总结而言,神经网络的本质是一个计算模型,它通过模拟生物神经元的连接机制,从数据中学习并识别特定模式。我们从单个神经元的输入与输出,到权重与偏置的动态调整,再到整个网络依据损失函数进行全局优化的过程,完整地梳理了其核心工作流。本文聚焦于神经网络的核心原理与概念框架,旨在为您建立一个清晰的认知基础。若希望深入探索其背后的数学细节与前沿应用,我们鼓励您在此基础上查阅更专业的文献。归根结底,只有深刻理解了底层原理,我们才能在面对未来的 AI 应用与挑战时,做到心中有数、从容不迫。
其他
这个网站通过交互式的可视化界面,生动地揭示了神经网络的内部运作过程:Tensorflow — Neural Network Playground